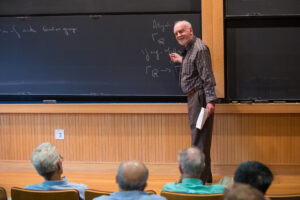
2018 में, डॉ. लैंगलैंड्स को प्रतिनिधित्व सिद्धांत को संख्या सिद्धांत से जोड़ने वाले उनके दूरदर्शी लैंगलैंड्स कार्यक्रम के लिए प्रतिष्ठित एबेल पुरस्कार मिला।
पांच वर्ष पूर्व, 2018 में, डॉ. लैंगलैंड्स को “संख्या सिद्धांत को प्रतिनिधित्व सिद्धांत से जोड़ने वाले उनके दूरदर्शी कार्यक्रम” के लिए गणितज्ञों के सर्वोच्च सम्मानों में से एक, एबेल पुरस्कार से सम्मानित किया गया था। यह अभूतपूर्व पहल, जिसे लैंगलैंड्स प्रोग्राम के नाम से जाना जाता है, की जड़ें डॉ. लैंगलैंड्स द्वारा 1967 में फ्रांसीसी गणितज्ञ आंद्रे वेइल को लिखे गए 17 पेज के एक पत्र में हैं, जिसमें अस्थायी विचारों की एक श्रृंखला सामने रखी गई है।
लैंग्लैंड्स कार्यक्रम की जटिलता
- यहां तक कि विकिपीडिया, जो जटिल विचारों को सरल बनाने के लिए जाना जाता है, मानता है कि लैंगलैंड्स कार्यक्रम “बहुत जटिल सैद्धांतिक अमूर्तताओं से निर्मित है, जिसे समझना विशेषज्ञ गणितज्ञों के लिए भी मुश्किल हो सकता है।”
- अपनी जटिलता के बावजूद, लैंगलैंड्स प्रोग्राम ने गणित के दो अलग-अलग क्षेत्रों: संख्या सिद्धांत और हार्मोनिक विश्लेषण के बीच संबंध स्थापित करने के अपने महत्वाकांक्षी लक्ष्य के साथ गणितीय समुदाय को मोहित कर लिया है।
संख्या सिद्धांत और हार्मोनिक विश्लेषण की समझ
I. संख्या सिद्धांत
- संख्या सिद्धांत, संख्याओं और उनके संबंधों का अंकगणितीय अध्ययन, सदियों से गणितीय अन्वेषण की आधारशिला रहा है।
- ऐसे संबंधों के उदाहरणों में पाइथागोरस प्रमेय (a² + b² = c²) जैसी मूलभूत अवधारणाएं शामिल हैं।
- इस क्षेत्र में गणितज्ञ पूर्णांक जैसे असतत अंकगणित से निपटते हैं, जो पूर्ण संख्याओं की दुनिया के भीतर छिपे रहस्यों को उजागर करते हैं।
II. हार्मोनिक विश्लेषण
- इसके विपरीत, हार्मोनिक विश्लेषण आवधिक घटनाओं के अध्ययन में गहराई से उतरता है, जो गणितीय वस्तुओं पर ध्यान केंद्रित करता है जो तरंगों की तरह प्रकृति में अधिक निरंतर होते हैं।
- जबकि संख्या सिद्धांतकार अलग-अलग तत्वों की जांच करते हैं, हार्मोनिक विश्लेषक आवधिक कार्यों और उनके अनुप्रयोगों की जटिलताओं को समझने की कोशिश करते हुए निरंतर क्षेत्र में नेविगेट करते हैं।
लैंग्लैंड्स कार्यक्रम का उद्देश्य
- लैंगलैंड्स कार्यक्रम के मूल में संख्या सिद्धांत और हार्मोनिक विश्लेषण के बीच गहरा संबंध खोजने का एक साहसिक प्रयास निहित है।
- कार्यक्रम की शुरुआत गणित की इन दो दूर की शाखाओं के बीच अंतर को पाटने की इच्छा से प्रेरित थी, जिनमें से प्रत्येक अपने सिद्धांतों और समस्याओं के अनूठे सेट के साथ थी।
ऐतिहासिक संदर्भ: एबेल और गैलॉइस
- लैंगलैंड्स कार्यक्रम की पूरी तरह से सराहना करने के लिए, उस ऐतिहासिक संदर्भ को समझना महत्वपूर्ण है जिसने इसे आगे बढ़ाने के लिए प्रेरित किया।
- 1824 में, नॉर्वेजियन गणितज्ञ नील्स हेनरिक एबेल ने 4 से अधिक घात वाले बहुपद समीकरणों के मूलों के लिए एक सामान्य सूत्र खोजने की असंभवता का प्रदर्शन किया।
- इस सीमा ने बहुपद समीकरणों के सार्वभौमिक समाधान खोजने वाले गणितज्ञों के लिए एक चुनौती पेश की।
- लगभग उसी समय, फ्रांसीसी गणितज्ञ एवरिस्ट गैलोइस स्वतंत्र रूप से एक समान निष्कर्ष पर पहुंचे।
- 1832 में, गैलॉइस ने सुझाव दिया कि सटीक मूलों पर ध्यान केंद्रित करने के बजाय, गणितज्ञ एक वैकल्पिक मार्ग के रूप में मूलों के बीच समरूपता का पता लगा सकते हैं।
- इस विचार ने गणितीय परिदृश्य में गहन संबंधों को उजागर करने की लैंगलैंड्स कार्यक्रम की आकांक्षा के लिए आधार तैयार किया।
जिज्ञासा की विरासत: लैंगलैंड्स कार्यक्रम का स्थायी प्रभाव”
- लैंगलैंड्स कार्यक्रम गणितज्ञों की स्थायी जिज्ञासा और सरलता के प्रमाण के रूप में खड़ा है।
- पांच दशक पूर्व लिखे गए एक पत्र से प्रेरित डॉ. लैंगलैंड्स की दूरदर्शी खोज, दुनिया भर के गणितज्ञों को संख्या सिद्धांत और हार्मोनिक विश्लेषण के बीच गहन अंतरसंबंध का पता लगाने के लिए प्रेरित करती रही है।
Find More Miscellaneous News Here

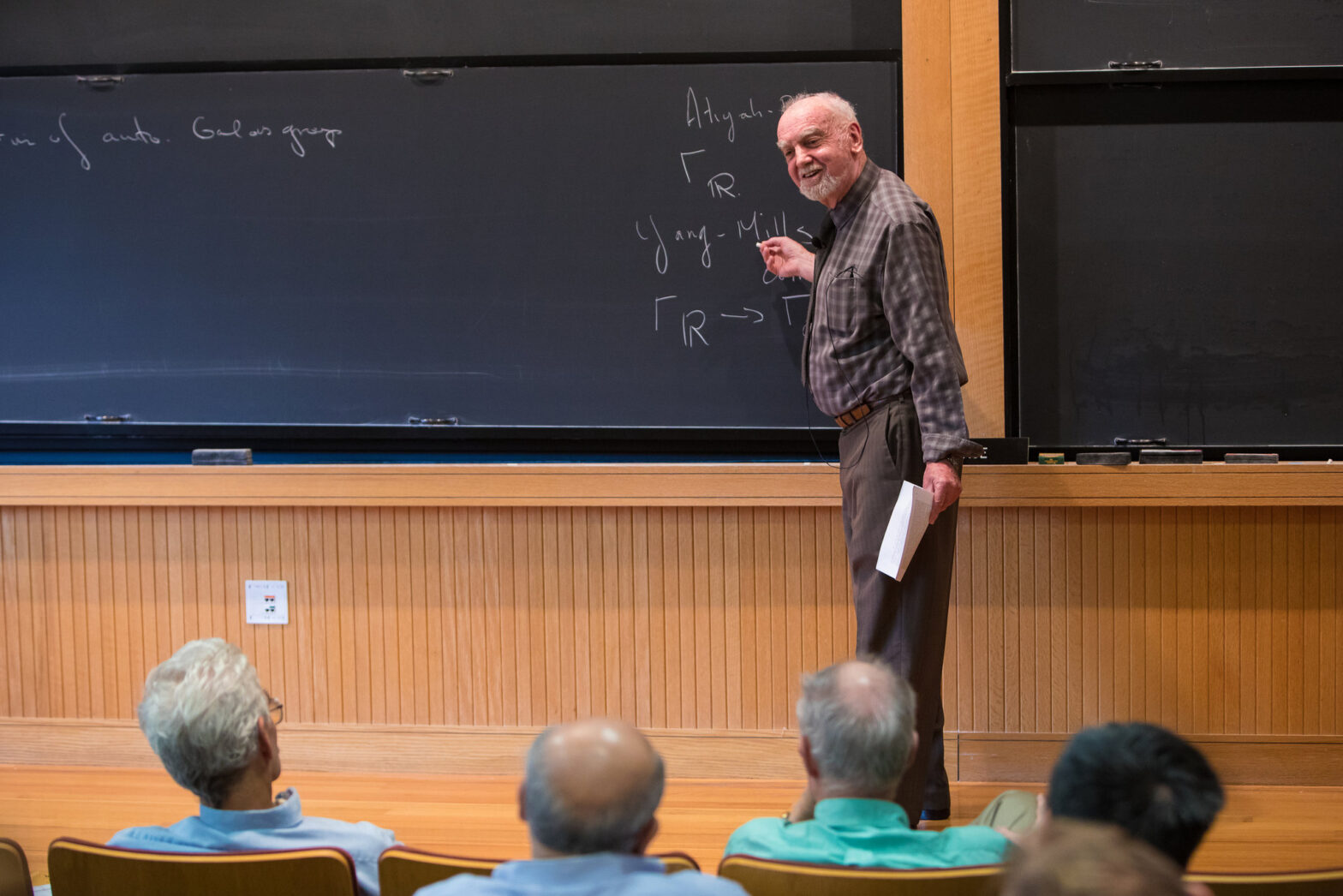


 CISF स्थापना दिवस 2026: तारीख, इतिहास और...
CISF स्थापना दिवस 2026: तारीख, इतिहास और...
 प्रधानमंत्री मोदी ने दिल्ली में भारत की ...
प्रधानमंत्री मोदी ने दिल्ली में भारत की ...
 FIFA वर्ल्ड कप 2026 का पूरा शेड्यूल: मैच...
FIFA वर्ल्ड कप 2026 का पूरा शेड्यूल: मैच...








